Poincaré is one of the greatest and most original mathematicians and physicists the world has ever seen. He came close to discovering special relativity before Einstein. He almost single-handedly created an extremely important branch of modern mathematics - algebraic topology. Poincaré's breadth of knowledge and remarkable achievements, his research covers several branches of mathematics, as well as celestial mechanics, modern physics, and even psychology, so he is called the last great scientific all-rounder in the world.
Much like Riemann, Poincare likes to start from basic principles and carry out his own research work, rather than base his research on other people's results or even his own previous work. Most mathematicians today consider him one of the greatest geniuses of all time. He also has a keen interest in the nature of mathematical thinking. In 1908, based on reflection on his own thought process, he gave a famous lecture on mathematical creativity entitled "The Invention of Mathematics".
Poincaré himself wrote:
We prove by logic and create by intuition.
He especially disagrees with Hilbert's view that mathematical reasoning can be axiomatic and (in principle) mechanized. It was a plan that Poincaré thought was impossible to succeed, and Gödel later proved him right.
Poincaré's first major contribution to mathematics was the creation of the concept and theory of automorphic functions, which is a special class of functions from complex numbers to complex numbers. In his subsequent career, Poincaré made further research on functions involving complex numbers, and he is generally credited as the founder of the theory of analytic functions of multiple complex variables. He also studied number theory and geometry.
Poincaré conjecture
In Poincaré's research on topology, a world problem arises the Poincaré conjecture. In 1895, Poincaré published his book "Analysis of Position". In this book, Poincaré introduced almost all concepts and main methods in topology. Topology is a kind of "hypergeometry". Mathematicians study very general properties of surfaces and other mathematical objects through topology. In topology, mathematicians are mostly interested in three-dimensional or higher-dimensional mathematical objects. Poincaré mistakenly believed that a fact that is obvious about two-dimensional objects will also be true for similar objects in three or higher dimensions. (This is where the Poincaré conjecture comes from). Two-dimensional topology is sometimes evocatively referred to as rubber-membrane geometry.
Rubber membrane geometry
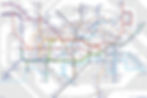
In 1931, Baker of England designed the current London Underground. This map is considered one of the best and many people tried to improve it without success. Combining convenience with beauty, the map has become a London icon and a model for tube maps around the world. This map shows the enormous power of topology. In fact, this map is inaccurate in every respect. But it describes exactly what a passenger needs from the map where to get on, where to get off, and where to change lanes at the expense of every other detail.
This example illustrates the nature of two-dimensional topology. If that subway map were printed on a sheet of rubber that was extremely elastic, it could be stretched and compressed just enough to get every detail right, resulting in a standard, geographically accurate map. In mathematical terms, the reason is that the layout of this network structure (defined as a collection of points connected by distinct straight lines) is a topological property. Simply put, networks are topological objects. You can twist and stretch any wire in a net without changing its overall layout. To change the network, you must break a connection or add a new one. This is true for circuit diagrams, circuits themselves, computer chips, telephone networks, and the Internet.
This is why rubber membrane geometry is one of the most important branches of mathematics in the world today. In the case of a subway map, it doesn't matter if it is cartographically accurate as long as it is topologically accurate. Similarly, for the design of a circuit or a computer chip, it is the layout of the network that matters. If the layout is topologically accurate, then the location of the wires can be freely changed to meet other design requirements. The same is true in the design of computer chips, where the key is that the circuits etched on the silicon must be topologically accurate.
Generally speaking, two-dimensional topology (rubber-membrane geometry) is the study of such a property of graphics: the graphics are drawn on an (imaginary) rubber membrane with excellent elasticity, and then the membrane is twisted and stretched, and this property remains unchanged. In fact, the development of topology was not driven by the needs of any field of applied mathematics. Instead, it comes from within pure mathematics, from the struggle to understand why calculus works.
Calculus and Topology
From the moment Newton and Leibniz invented calculus in the mid-17th century, mathematicians have used it extensively. However, no one really understands why calculus works. After 300 years of work by a large group of mathematicians (who performed detailed analyzes of the nature of real numbers and infinite processes, as well as mathematical reasoning itself), this has finally been explained.
But it also makes mathematics more and more abstract. The 19th century saw the emergence of a multitude of new types of objects and patterns that were not part of everyday experience. Among the new objects and new models studied by mathematicians in the last 200 years, there are non-Euclidean geometry (parallel lines can intersect), four-dimensional and higher-dimensional geometry, infinite-dimensional geometry, algebra that uses symbols to represent the symmetry of figures (called group theory), the algebra that uses symbols to represent logical thought (propositional logic), and the algebra that uses symbols to represent motion in two or three dimensions (vector algebra).
In the expansion of abstraction, topology also appeared. The original idea was to invent a kind of "geometry" to study the properties that graphics will not be destroyed by continuous deformation, so this geometry does not depend on concepts such as straight lines, circles, and cubes, nor does it depend on length, area, and volume, Angle these measures. In topology, the object of study is called a topological space.

The connection between topology and how calculus work" is tenuous. In essence, both rely on being able to grasp the infinitesimal. But what does a topological transformation have to do with infinitesimals? The key is: intuitively speaking, the essence of topological transformation is that two points that are "infinitely close" before the transformation remain " infinitely close after the transformation. In particular, no matter how stretched, compressed or twisted a piece of rubber film will not destroy this closeness. Two points that are initially close to each other remain close after the operation is complete.
Note that the concept of closeness mentioned here is relative to all other points in the topological space. We can stretch the membrane so that two points that were initially close together no longer appear close together to us. But in this case, the "proximity" change is a geometric change that we impose from the outside. From the perspective of the rubber membrane, the two points are still close together.
The only way to break proximity is to cut or tear the membrane an operation forbidden in topology.
The problem with this approach is that the concept of "infinite proximity" is not a well-defined concept. However, by thinking about topological transformations in this way, mathematicians have found a way to give a precise definition of topological transformations (don't expect me to give a definition here). At this time, the concept of topological transformation can be used to accurately analyze the intuitive concept of the infinite approach. In this way, they developed calculus in a rigorous sense.
This is the main reason why Poincaré and other mathematicians created topology. A question arises in the mind of anyone encountering topology for the first time: about topological spaces. Not only does a topological space have no straight lines, but it also has no notion of a fixed shape, nor does it have distances of any kind. All you can tell is when two points are close to each other.
There are many more that you didn't expect

Topology is one of the most colorful, fascinating, and important branches of contemporary mathematics, with many applications in mathematics, physics, and other fields. Only one important application is mentioned here: topology is the mathematical foundation of superstring theory, and superstring theory is the latest theory about the nature of the universe.
Let's take a look at what topologists study. For simplicity, I restrict myself to the two-dimensional case. And think about what properties in high school geometry can be transferred to the topology. Because stretching and twisting a rubber membrane turns straight lines into curves and changes distances and angles, these familiar geometric concepts mean nothing in topology.
So what's left? There are also lines and closed loops (rings). If you draw a circle on an extremely elastic rubber membrane, no matter how much you stretch, compress, and twist the rubber membrane, the circle will still be a circle. What else?
To answer this question, We'll show you the first topology result. It is attributed to the great Swiss mathematician Euler. In 1735, Euler solved a long-standing problem - the Königsberg bridge problem. Many citizens of Konigsberg are used to walking here with their families, and they often have to cross several bridges. So there is a question that is often discussed: Is there a route that happens to only cross each bridge once?

Euler realized that the exact location of the islands and bridges was irrelevant, what mattered was how the bridges were connected, that is, the network formed by the bridges. This problem is a topology problem, not a geometry problem.
So Euler argues as follows. Take any network, assuming that there is a travel route, and it happens that each edge is only traversed once. Any node, as long as it is not the starting point or end point of this route, must have an even number of edges intersecting here, because these edges can be paired in a way that one path enters and one exits. But in this network of bridges, those 4 vertices all have an odd number of edges intersecting there. Hence no such route is possible. The conclusion is that a route that passes every bridge in Königsberg exactly once does not exist.

This solution to the Königsberg bridge problem yielded the world's first topology theorem. Euler proved that for any network drawn on a plane, if V is the total number of vertices (nodes), E is the total number of edges (or links), and F is a "face" (consisting of 3 or more edges the total number of enclosed areas), then the following simple formula holds:

For example, for the network of the Königsberg bridge, there are V=4, E=7, and F=4, so

Although Euler solved the first topology problem and proved the first topology theorem, it wasn't until the late 19th century that topology really took off. Because at this time, Poincaré made his debut!
Through the surface
In topology, we study the properties of shapes and objects that remain invariant under continuous deformation. By continuous we mean that this deformation does not involve any cutting, tearing, or sticking. For example, in topology, footballs are the same as footballs, and they are the same as tennis balls since any of these three balls can be transformed into the other two by successive deformations. There is only one kind of "ball" in topology. The differences between the various types of balls that we usually recognize are related to size and shape, but these are not topological properties.
Early studies in topology were looking for ways to tell when two shapes were topologically different, and Poincaré was a leading figure in this quest. For example, any sphere is topologically different from any torus, although any two spheres are topologically identical, as are any two tori (circular, elliptical, or whatever). Intuitively, this seems obvious. After all, there seems to be no way you can continuously transform a sphere to get a torus. The problem is that insignificant word - as if. How do you know there is definitely no way to do this? E.g,

In the ring-dividing puzzle shown above, can you find a way to continuously transform the graph (a) into the graph (b)? The easy way to think of it is to cut off one of the two interlocking rings (but this is not allowed), as shown in (c). But it can be done without cutting the ring. This should convince you that finding various perfectly reliable ways to prove that two objects are topologically identical or different is indeed an important task.
By the way, just by not being able to find a continuous deformation that transforms one object into another, it is not conclusive that the two objects are topologically different. What's needed here is to find some topological property that one of the two objects has and the other doesn't that is, a property that remains the same through successive deformations.
We have already encountered one such property. For any network, the value of V - E + F is a topological property. This amount is the same for any network.
For a grid on a two-dimensional plane, V - E + F = 1; for a network on a sphere (to cover the entire sphere, not a part of the sphere), V - E + F = 2; and for a network on the torus (also required to cover entire torus), V-E+F =0. We can then assert with absolute certainty that the two-dimensional plane, sphere, and torus are topologically different. For a network drawn on a double torus (shaped like a number 8), V-E+F=-2, so we also know that a double torus is topologically different from a plane, a sphere, and a torus.
For an arbitrary network drawn on a particular surface, the value of the expression V-E+F is an example of what mathematicians call a topological invariant of a surface. If we topologically transform (i.e. continuously deform) this surface, this value will remain the same. To commemorate Euler's contribution, people call the value of V-E+F the Euler characteristic number of the surface. Topologists have discovered many topological invariants that can be used to determine whether two specific surfaces are topologically equivalent, and Euler's characteristic is one of them.

Another topological invariant is the chromatic number of a surface. It originated from a classic problem about map coloring. In 1852, a young English mathematician named Guthrie posed a seemingly trivial problem:
What is the minimum number of colors you need in order to be able to color areas on any given map?
The only rule is that any two regions that share a common border must be colored differently. (If two regions touch each other at only one point, then that point cannot be considered a common boundary.) It is easy to draw a map that requires four different colors, but is there a map that requires five colors? The answer is no, but it took mathematicians more than 100 years to prove it, and the proof involved not only ingenious mathematical reasoning but also significant applications of computers. In fact, the four-color theorem was the first mathematical conjecture thought to require a computer to be proved.

The four-color theorem is clearly a consequence of topology since successive deformations of the paper on which the map is drawn do not alter the pattern of shared boundaries. Two regions that share a common boundary before deformation will still do so after deformation, and vice versa.
The four-color theorem, and the original question it answers, are for maps drawn on a flat surface. But you can ask the same question about maps drawn on any surface. The chromatic number of a surface is the minimum number of colors required to color any map drawn on the surface. According to the four-color theorem, the chromatic number of a plane is 4. The chromatic number of the sphere is also 4. The chromatic number of the torus is 7.
Side issues
Another topological invariant arises from the notion of "sidedness" whether a surface has one side or two. Any curved surface has two sides, doesn't it? The answer is no. It is easy to construct a surface with only one side. Take a long thin strip of tissue paper, twist it half a turn, and glue the ends together to form a twisted circle of paper.

This twisted circle of paper is a surface with only one side, and it is called a Möbius strip. In addition to having only one side, a Möbius strip also has only one side.
Mobius took this example to tell us that laterality is closely related to laterality. Usually, mathematicians focus on surfaces that have no edges - they call them closed surfaces. Also, the more interesting topological properties have to do with the internal structure of surfaces (how they twist and flip). In fact, for every surface with one or more edges, there generally exists a closed surface with almost the same properties. For example, a sphere and a finite plane (such as a flat tabletop) are similar in nature. When we prove a topological result on a sphere, we usually immediately have a result on a plane, and vice versa.
Intuitively, this is because we can take a flat piece of perfectly stretchable paper and gather its edges together to form a closed bag topologically, this is a sphere.
The closed surface corresponding to the Möbius strip is called a Klein bottle. A Klein bottle has no rim and has neither an interior nor an exterior. Theoretically, you could take two Möbius strips, glue them together along their single edge, and form a Klein bottle. I say " in theory " because you can't do this in ordinary 3D space. The Klein bottle (as an object of mathematics) exists only in four dimensions. In our three-dimensional world, you'd better allow the surface to pass through itself,
In four-dimensional space, the bottle does not necessarily pass through itself. To ordinary people, an object that exists only in four dimensions is certainly not real, but mathematicians don't think so. After all, everyone "knows" that negative numbers don't have square roots, but that hasn't stopped mathematicians from inventing complex numbers and using them in practical applications. Much of the great power of mathematics comes from the fact that:
We can use it to study objects beyond those conceived by living beings in the three-dimensional world.
For example, we can study the properties of networks drawn on Klein bottles. We found that the Euler characteristic of the Klein bottle is 0, the same as the torus. Does this mean that the Klein bottle and the torus are topologically equivalent? no! Euler's characteristic number cannot distinguish the Klein bottle from the torus, but the chromatic number can, the chromatic number of the Klein bottle is 6, and the torus is 7.
The topological property of the Klein bottle "corresponds to the one-sidedness of its surface" is a fancy concept called non-orientability. It means that on the surface of a Klein bottle you cannot distinguish left-handedness from right-handedness or clockwise rotation from counterclockwise rotation. If you draw a left hand on the surface of a Klein bottle, and then slide the figure far enough along the surface (far enough means that if the Klein bottle is in three-dimensional space, then the hand completely passes through the self-intersection bottleneck), when it returns to the starting point, you will find that it has magically become a right hand.
This experiment is easier to do on the Möbius strip. Draw a small left hand on this surface, then copy the shape next to it, and repeat the process until you are back to your starting point. At this time, you will find that this left hand has become a right hand. Alternatively, draw a small circle on the surface of a Klein bottle or a Möbius strip, with an arrow for a clockwise rotation, and if you slide or copy this shape along the surface until you return to the starting point, you will find that the arrow is pointing counterclockwise.

Surfaces that cannot be changed from left to right or from clockwise to counterclockwise by sliding along the surface are said to be orientable. For example, a sphere (or plane) is orientable, as are torus and double torus. A surface capable of such changes, such as a Klein bottle or a Möbius strip, is said to be non-orientable. Orientability (or non-orientability) is a topological invariant.
Surface classification
One of the first results of topology is to prove that any two closed surfaces can be distinguished as long as there are two topological invariants, Euler characteristic number, and orientability. That is, two closed surfaces are de facto equivalent if they have the same Euler characteristic and both are orientable or both are non-orientable. This result is called the Surface Classification Theorem because it says that you can classify all surfaces (in the topological sense) using just these two features.
In short, the proof of the surface classification theorem is made by taking the sphere as the fundamental surface and evaluating how much any given surface differs from the sphere (that is, what has to be done to the sphere in order to transform the sphere into that surface). This is consistent with our intuition: the sphere is the simplest and most basic closed surface.

In this case, the operations performed on the sphere in order to transform it into some other curved surface go beyond the conventional topological operation of a continuous deformation. Indeed, if you alter a sphere by twisting, bending, stretching, and compressing, the resulting object is still topologically a sphere. To figure out how surfaces are constructed from spheres to classify surfaces, one must allow cutting and stitching in addition to the usual twisting, stretching, etc. Topologists call this process cutting. A typical circumcision procedure involves cutting a piece or pieces from the sphere, twisting, flipping, stretching, or compressing the pieces, and then sewing the pieces back onto the sphere.
The classification theorem tells us that any orientable surface is topologically equivalent to a sphere with a certain number of " handles " stitched on its surface. You can get a ring handle by cutting two holes in a sphere and connecting them with a pipe, as shown on the left in the picture below, any non-orientable surface with a sphere sewn with a certain number of "intersecting sets", etc. price. You can get a cross sleeve by cutting a hole in the sphere and sewing a Möbius strip around the edge of the hole, as shown on the right in the picture below. As in the case of the Klein bottle, this cannot be done in ordinary three-dimensional space without the Möbius strip passing through itself.

The Surface Classification Theorem says that any smooth closed surface is topologically equivalent to a spherical surface with a certain number of shanks or intersections.
In the early 20th century, Poincaré and other mathematicians set out to classify higher-dimensional analogs of surfaces, which they called "manifolds." The approach they attempted was similar to that already effective for two-dimensional surfaces. They take as a basis a three-dimensional analog of a sphere (called a "three-manifold") and try to classify all three-manifolds by measuring how much any three-manifold differs from this three-manifold (referred to as a 3-manifold).
Note that a regular surface, such as a sphere or torus, is a two-dimensional object. Although the portion enclosed by this surface is three-dimensional, the surface itself is two-dimensional.
Any curved surface other than a plane can only be constructed in three-dimensional or higher-dimensional space. Thus, any closed surface requires a three-dimensional or higher-dimensional space. For example, constructing a sphere or a torus will take a three-dimensional space, and constructing a Klein bottle will take a four-dimensional space. However, a sphere, a torus, or a Klein bottle are all two-dimensional objects a curved surfaces with no thickness that could, in principle, be made from a flat, extremely elastic sheet.
But just as a sphere can be thought of as a two-dimensional analog (in three dimensions) of a circle (which is a one-dimensional object - a curve, in two dimensions), we can likewise conceive of a three-dimensional analog of a sphere ( in a four-dimensional space). Of course, we can't imagine it in practice. But we can write equations that determine such an object and study it mathematically. In fact, physicists usually study such imagined objects and use these results to help understand the universe we live in. 3-manifolds, the three-dimensional analogs of curved surfaces (existing in spaces of four or more dimensions), are sometimes called hypersurfaces, while the three-dimensional analogs of spheres are called hyperspheres.

You can write equations that determine manifolds in three, four, five, six, or any number of dimensions. The mathematical theories of matter that physicists currently study view our universe as having 11 dimensions. According to these theories, we are directly aware of 3 of these dimensions. Other dimensions manifest themselves as various physical properties such as electromagnetic radiation and the forces that hold atoms together.
Poincaré attempted to classify three-dimensional and higher-dimensional manifolds by taking the "sphere" of each dimension as a basic graph and then applying the cut-and-fill technique. The natural first step in this attempt is to find a simple topological property that tells you when a given (hyper)surface is topologically equivalent to a (hyper)sphere.
Remember, what we're doing here is topology. Even in the simple case of regular 2D surfaces, a surface can appear extremely complex and still turn out to be a sphere through continuous deformation.
In the case of two-dimensional surfaces, there is such a property. Suppose you take a pencil and draw a simply closed circle on a sphere. Now imagine the circle shrinking smaller and smaller, keeping sliding on the sphere as it shrinks. Is there a limit to how small this circle can shrink? Obviously not. You can shrink the circle so that it is indistinguishable from a point. Mathematically, you can literally shrink it down to a point.
The same thing doesn't necessarily happen if you start by drawing a circle on a torus. The property that a circle is drawn arbitrarily on a curved surface can shrink to a point is a surface topological property that only spherical surfaces have. That is to say, if there is a surface on which every loop ("every" is important here) can shrink to a point without leaving the surface, then this surface is equivalent to the spherical topology.
Is this also true for a three-dimensional hypersphere? This was the question Poincaré posed in the early 20th century, his first step on the road to a classification theorem for three-dimensional hypersurfaces. He developed a systematic approach (called homotopy theory) to study what happens to loops as they move and deform on a manifold.
In fact, this is not the case. At first, Poincaré postulated that the loop-contraction properties of three-manifolds were indeed characteristic of three-dimensional spheres. After a while, however, he realized that his assumptions might not be true. In 1904, he published his question,
Consider a three-dimensional compact manifold V without boundary, even if V is not the same embryo as a three-dimensional sphere, can the fundamental group of V be trivial?
Dimensionality reduction means, Is it possible that a three-dimensional manifold with the property of loop contraction is not equivalent to a three-dimensional sphere?
The Poincaré conjecture was born!
In 1960, the American mathematician Stephen Smale proved that the Poincaré conjecture is correct for all manifolds of five dimensions and above. Thus, if a five-dimensional or higher-dimensional manifold has the property that any closed loop drawn on it can be shrunk to a point, then this manifold is topologically equivalent to a hypersphere of the same dimension.
Unfortunately, the method used by Smale cannot be applied to three- or four-dimensional manifolds, so the original Poincaré conjecture remains unsolved. Later, in 1981, another American, Friedman, discovered a way to prove the Poincaré conjecture on 4-manifolds.
The problem is not solved. The Poincaré conjecture has been proven to be true for every dimension except three. Both Smail and Friedman received Fields Medals for their achievements. Whoever first proves this only remaining case of the Poincaré conjecture will undoubtedly receive the same credit.
In 2003, Russian mathematician Grigory Perelman proved the three-dimensional case of the Poincaré conjecture. In 2006, the mathematical community finally confirmed that Perelman's proof solved the Poincaré conjecture.